Aristotle's On Interpretation Ch. 10. segm. 19b31-19b36 & 20a16-20a30: Notes on the formulation of universal and non-universal assertions, the relations of opposition and implication among them
(19b31-19b36 & 20a16-20a30) of Ch. 10: Notes on the formulation of universal and non-universal assertions, the relations of opposition and implication among them
The subject of an assertion may be a particular such as “Socrates” (e.g. Socrates is wise) or a universal such as “man” (e.g. man is wise). Now, as Aristotle instructed us in Ch. 7 17a37-11b16, a particular is something which presents itself as a single, one-of-a-kind thing. A universal, on the other hand, presents itself as a thing insofar as we find it instantiated across many particulars.
We are hence able to assert something of a universal in two different ways: (i) universally, i.e. of all the things in which the universal instantiates itself, or (ii) non-universally, i.e. of some of those things.
(i) to assert something universally of a universal means to either affirm or deny something of the sum of things which instantiate that universal, i.e. all those things which accept the subject of our assertion as a predicate (e.g. given that the assertions “Socrates is a man” and “Kallias is a man” are true, when we assert something of “man” we also assert it of Socrates and Kallias). For this reason, we add (a) “every” before the subject to signify the inclusion of all the things the universal encompases (e.g. every man is wise) and (b) “no” to signify the exclusion of those things (e.g. no man is wise) from what the predicate signifes.
(ii) to assert something non-universally of a universal means to affirm or deny something of a part of the things which instantiate that universal. Put differently, as long as we do not strictly assert something of all or none of the things which accept that universal as predicate, we assert it non-universally. In his examples, the philosopher draws our attention to three different ways in which we may assert something non-universally of a universal. Namely, he either (a) quantifies the subject with “not every” (e.g. not every man is wise), or (b) “some” (e.g. some man is wise), or (c) he does not quantify the subject at all (e.g. man is wise).
(a) With “not every” before the subject of our assertion, we signify the exclusion of what the predicate signifies from at least part of the things the universal subject encompasses. The “not” denies the “every”. Hence, if it is true to assert that “not every man is wise”, then the assertion “every man is wise” is false and the other way around.
(b) With “some” before the subject, we convey the inclusion of what the predicate signifies from at least a part of the things the universal encompasses. As such, if it is true to assert that “some man is wise”, then the assertion “no man is wise” is false and vice versa.
(c) When we forego quantifying the universal subject of our assertion (man is wise), we leave indeterminate the extent in which the predicate applies across those things the universal subject encompasses. In doing so, we do not assert the predicate of any concrete set of things which instantiate that universal but rather of the universal itself. In other words, the assertion we produce is a generality. This allows for contradictories (e.g. man is wise - man is not wise) to be true or false together.
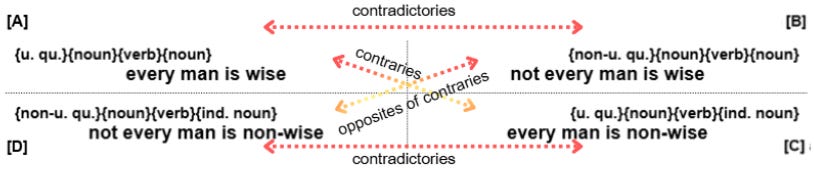
Sketching out the relations of opposition between two contradictory pairs of assertions in which one assertion is a universal affirmation and the other a non-universal negation. The assertions have three constitutive elements. In one pair the predicate combines “is” with a noun, in the other the indefinite counterpart of that noun
The present diagram is diferent to those we drew for assertions with a particular subject and assertions with a universal subject only applied non-universally. To begin with, unlike the previous assertions, each of the four assertions in this diagram accompanies its subject with a quantifier.
As we may observe, both affirmations [A] and [C] quantify their subject (man) with “every”. Each thereby asserts its predicate (either “is wise” or “is non-wise”) of “man” universally. Negations [B] and [D], on the other hand, quantify the subject with “not every”. They thus assert their predicate of “man” non-universally. In On Int. Ch. 7 Aristotle calls the former universal affirmations [uA], the latter non-universal negations [nN].
The non-universal negations [B] and [D] do not feature the indefinite “is not” in their formulation. That is, they do not deny their predicate of “every man”. Instead, they modify “every” with “not” and therewith deny the universality of what they assert. That is, they deny the affirmation of the predicate to everything the universal “man” encompasses as such. Put differently, by way of the quantifier “not every”, [B] and [D] signify that their predicate does not apply to at the very least one instance of the subject “man”.
Notes on the relations of implication between (i) universal affrimations and universal negations, (ii) non-universal affirmations and non-universal negations
(i) each universal affirmation implies a universal negation
In On Int. Ch. 10 20a16-20a30 Aristotle instructs us that each universal affirmation [uA] implies a universal negation [uN]. With this, we mean that the underlying circumstances that necessitate the truth of what a universal affirmation conveys also allow for the truth of a universal negation. For example, if the [uA] “every man is wise” is true, then the [uN] “no man is non-wise” is true as well. Further, if “every man is non-wise” is true, then “no man is wise” is also true.
In the present text, the philosopher formulates each [uA] by quantifying the subject “man” with “every”, then combining it with “is” and a noun or an indefinite noun (e.g. “wise” or “non-wise”). In order to formulate the implied [uN] we swap “every” with “no” and replace the predicate noun with its indefinite counterpart or vice versa.
Now, Aristotle describes “every man is wise” as contrary to “no man is wise”. He elaborates that two assertions are contrary when they can never be true together, yet may happen to be false at the same time. With this in mind, we may come to the conclusion that “every man is non-wise” is also contrary to “every man is wise”. Further, that “no man is wise” is also contrary to “no man is non-wise”.
(ii) each non-universal negation follows from a non-universal affirmation
Aristotle further instructs us that each non-universal negation [nN] follows from a non-universal affirmation [nA]. By this, we understand that the underlying circumstances which necessitate the truth of a given non-universal affirmation also allow for the truth of a non-universal negation. If ”some man is wise”, then it follows that “not every man is non-wise”. Furthermore, if “some man is non-wise”, then it follows that “not every man is wise”.
To formulate each [nN], Aristotle quantifies the subject “man” with “not every”. He then combines it with “is” and a noun or an indefinite noun (e.g. “wise” or “non-wise”). In order to formulate the [nA] from which a given [nN] follows, we swap “not every” with “some” and replace the predicate noun with its indefinite counterpart or vice versa.
In On Int. Ch. 7 17b17-17b26, Aristotle describes the relation of opposition between assertions such as “some man is wise” and “not every man is wise” as the one between opposites of contraries. He explains that assertions which oppose each other thusly may happen to be true together, yet can never be false at the same time. In view of this, we may regard “some man is wise” to also oppose “some man is non-wise” as opposites of contraries. Further that “not every man is wise” opposes “not every man is non-wise” in the same way.
So far, we have discussed what universal and non-universal assertions are and how to formulate them. Furthermore, we considered which of these assertions oppose which and in what way. Finally, we examined what assertions follow from other assertions by way of implication.
Key points: (i) Assertions with a universal subject may be asserted universally or non-universally. (ii) To assert something universally of a subject means to assert it of the sum of things which instantiate it. To assert something non-universally means to assert it of part of those things. (iii) Provided our assertions signify the same thing of the same thing, (a) a universal affirmation will contradict with a non-universal negation, (b) a universal negation will contradict with a non-universal affirmation, (c) a universal affirmation will be contrary to a universal negation, (d) a non-universal affirmation will be the opposite of a contrary to a non-universal negation. (iv) A universal affirmation which combines “is” and a noun to form its predicate will imply a universal negation which combines “is” with the indefinite counterpart of that noun. If the predicate of the universal affirmation combines an indefinite noun, then the universal negation it implies will combine its noun counterpart. (v) A non-universal affirmation which combines “is” with a noun to form its predicate will imply a non-universal negation which combines “is” with the indefinite counterpart of that noun. If the predicate of the non-universal affirmation combines an indefinite noun, then the non-universal negation it implies will combine its noun counterpart.